JUINTINATION
APSP(All-pairs shortest paths) 본문
APSP(All-pairs shortest paths) 알고리즘이란?
어떤 그래프에서 모든 노드(시작 노드)부터 각각의 노드(도착 노드)까지의 모든 최단거리를 구하는 알고리즘이다.
여러 APSP 알고리즘 중에서 2가지를 살펴보겠다.
- 모든 정점에서 SSSP 알고리즘 실행하기
- 모든 정점에서 SSSP 알고리즘을 실행해야 하기 때문에 |V| 만큼 시간 복잡도가 증가한다.
- Dijkstra’s algorithm(음의 간선 X): O(|V||E| + |V|² log |V|)
- Bellman-Ford algorithm(음의 간선 O, 음의 사이클 X): O(|V|²|E|)
- DAG Shortest Path using Topological Sort: O(|V|² + |V||E|)
- 모든 정점에서 SSSP 알고리즘을 실행해야 하기 때문에 |V| 만큼 시간 복잡도가 증가한다.
- 음의 사이클이 존재하지 않는 경우
- Floyd-Warshall algorithm: O(|V|³) ≅ O(|V||E|)
플로이드 워셜 알고리즘(Floyd-Warshall Algorithm)
floyd_warshall(G) {
c[v][v] ← ∞ for all v ∈ V
c[u][v] ← w(u, v) for all w(u, v) ∈ E
for k ← 1 to |V|
for i ← 1 to |V|
for j ← 1 to |V|
if c[i, j] > c[i, k] + c[k, j]
then c[i, j] ← c[i, k] + c[k, j]
}의사 코드는 위와 같이 아주 간단하게 생겼다. 해석해보자면 i에서 j로 가는 기존의 최단경로보다 k를 거쳐서 가는 경로가 더 짧은 경우 i에서 j로 가는 최단경로의 값을 k를 거쳐서 가는 것으로 수정하는 과정을 반복하는 것이다.
모든 경로를 출력하기 위해선 위의 알고리즘을 다음과 같이 수정할 수 있다.
floyd_warshall(G) {
c[v][v] ← ∞ for all v ∈ V
c[u][v] ← w(u, v) for all w(u, v) ∈ E
next[u][v] ← v for all e(u, v) ∈ E
for k ← 1 to |V|
for i ← 1 to |V|
for j ← 1 to |V|
if c[i, j] > c[i, k] + c[k, j]
then c[i, j] ← c[i, k] + c[k, j]
next[i][j] ← next[i][k]
}
shortest_path(u, v) {
if next[u][v] = null
then return []
/* 연결리스트 P에 u 연결 */
while u ≠ v
u ← next[u][v]
/* 연결리스트 P의 맨 뒤에 u 연결 */
return P
}이해를 돕기 위해 백준 문제를 첨부한다. https://www.acmicpc.net/problem/11780
11780번: 플로이드 2
첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가
www.acmicpc.net
import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
final static int INF = Integer.MAX_VALUE / 2;
static int n, m;
static int[][] c;
static Integer[][] next;
public static String floydWarshall() {
StringBuilder sb = new StringBuilder();
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (c[i][k] + c[k][j] < c[i][j]) {
c[i][j] = c[i][k] + c[k][j];
next[i][j] = next[i][k];
}
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
sb.append(c[i][j] != INF ? c[i][j] : 0).append(" ");
}
sb.append("\n");
}
for (int u = 1; u <= n; u++) {
for (int v = 1; v <= n; v++) {
if (next[u][v] == null) {
sb.append(0);
} else {
ArrayList<Integer> path = new ArrayList<>();
path.add(u);
int tmp = u;
while (u != v) {
u = next[u][v];
path.add(u);
}
sb.append(path.size()).append(" ");
for (Integer e : path) {
sb.append(e).append(" ");
}
u = tmp;
}
sb.append("\n");
}
}
return sb.toString();
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
m = Integer.parseInt(br.readLine());
c = new int[n + 1][n + 1];
next = new Integer[n + 1][n + 1];
for (int i = 1; i <= n; i++) {
Arrays.fill(c[i], INF);
c[i][i] = 0;
}
while (m-- > 0) {
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
c[a][b] = Math.min(c[a][b], cost);
next[a][b] = b;
}
System.out.print(floydWarshall());
}
}
위의 플로이드-워셜 알고리즘을 관계식으로 나타내면 다음 그림을 그릴 수 있다.

그렇다면 이 관계식을 조금만 수정하여 어떤 그래프에서 모든 노드(시작 노드)부터 각각의 노드(도착 노드)까지 갈 수 있는 경로가 존재하는지 여부를 확인할 수 있을까? 답은 간단하다. 위의 그림에서 파란색 부분만 다음과 같이 수정하면 된다.

i에서 j로 가는 경로가 있거나(OR) i에서 k로 가는 경로와 k에서 j로 가는 경로가 둘 다 있으면(AND) i에서 j로 갈 수 있는 경로가 존재하는 것이다. 그렇다면 각 노드간 경로의 개수를 구할 수 있을까? 마찬가지로 답은 간단하다. 위와 똑같이 파란색 부분만 다음과 같이 수정하면 된다.
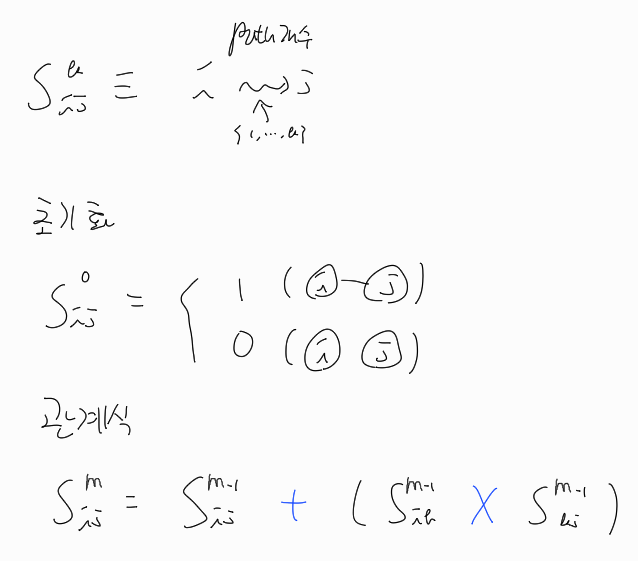
i에서 j로 가는 경로의 개수와 i에서 k로 가는 경로의 개수와 k에서 j로 가는 경로의 개수를 곱한 값을 더하면 i에서 j로 가는 경로의 총 개수가 나올 것이다. 마지막으로 각 노드간 경로의 개수가 딱 1개인 경우만 구할 수 있을까? 예상했듯이 위와 똑같이 파란색 부분만 다음과 같이 수정하면 된다.

XOR 연산은 배타적 논리합을 나타내는데 이는 2개의 명제 가운데 1개만 참일 경우를 판단하는 논리 연산이다. 예를 들어 c = a XOR b에서 c는 a가 참, b가 거짓이거나 a가 거짓, b가 참일 때만 참이다. a, b 둘 다 참이거나 거짓인 경우는 거짓이다. i에서 j로 가는 경로의 개수가 1개이거나 i에서 k로 가는 경로의 개수와 k에서 j로 가는 경로의 개수가 모두 1개면 i에서 j로 가는 경로의 개수가 딱 1개인지 여부를 확인할 수 있을 것이다.
그렇다면!! 위의 내용을 응용하여 각 노드간 경로의 개수가 2개 이상인 경우에는 어떻게 표현해야할까?
답은 아래 더보기에 넣어두었으며 참고하면 좋을 것 같다.
각 노드간 경로의 개수가 2개 이상인 경우 구하기
경로는 존재하지만 경로의 개수는 1개가 아니어야 한다.
NOT 연산과 AND 연산을 사용해도 좋지만 맨 아래 적혀있는 증명에 의하여 XOR 연산 1개만 사용하여 해결할 수도 있다.

'자료구조 및 알고리즘' 카테고리의 다른 글
| SSSP(Single-source shortest paths) (0) | 2023.08.06 |
|---|---|
| 위상정렬(Topological Sort) (1) | 2023.08.05 |
| 최소 신장 트리(Minimum Spanning Tree) (0) | 2023.07.31 |
| 해시 테이블(Hash Table) (0) | 2023.07.24 |
| 유니온 파인드(Union-Find) (0) | 2023.07.23 |
