JUINTINATION
최소 신장 트리(Minimum Spanning Tree) 본문
최소 신장 트리(MST)란?
- 가중치 그래프에서 사이클 없이 모든 점들을 연결시킨 트리들 중 선분들의 가중치 합이 최소인 트리
- 즉, 어떤 가중치 그래프의 신장 트리 중 선분들의 가중치 합이 최소인 트리
- 신장 트리는 그래프에서 사이클 없이 모든 점들을 연결시킨 트리로 주어진 그래프의 신장 트리를 찾으려면 사이클이 없도록 모든 점을 연결시키면 된다.
- 신장 트리는 그래프에서 사이클 없이 모든 점들을 연결시킨 트리로 그래프의 점이 n개 있다면 신장 트리에는 n-1개의 선분이 있다.
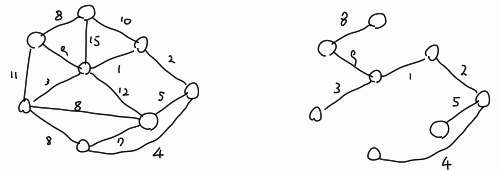
다음 예시에서 왼쪽 그림의 그래프의 최소 신장 트리는 오른쪽 그림의 그래프와 같다.
MST를 찾기 위한 알고리즘
최소 신장 트리를 찾는 대표적인 그리디 알고리즘으로는 크루스칼 알고리즘(Kruskal's Algorithm)과 프림 알고리즘(Prim's Algorithm)이 있다.
- 크루스칼 알고리즘
- 가중치가 가장 작은 선분이 사이클을 만들지 않을 때에만 트리에 선분을 추가시킨다.
- 의사 코드는 다음과 같으며 위의 예시를 구하는 과정은 그 다음 그림과 같다.
kruskal(G) {
Q ← E // 우선순위 큐 Q에 모든 간선 E를 삽입
T ← ∅ // 트리 T를 선언
while T의 edge 수 < n-1
// Q에 남은 간선 중 가중치가 가장 작은 간선 e
e ← EXTRACT-MIN(Q)
e를 T에 추가
if e가 T에 추가되어 사이클을 만들지 않으면
T에 e 추가
}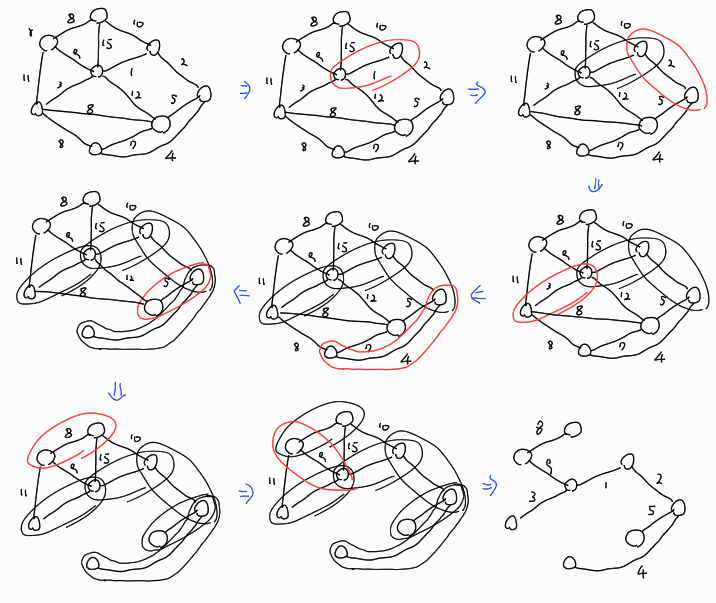
- 프림 알고리즘
- 주어진 가중치 그래프에서 임의의 점 하나를 선택한 후, (n-1)개의 선분을 하나씩 추가시켜 트리를 만든다.
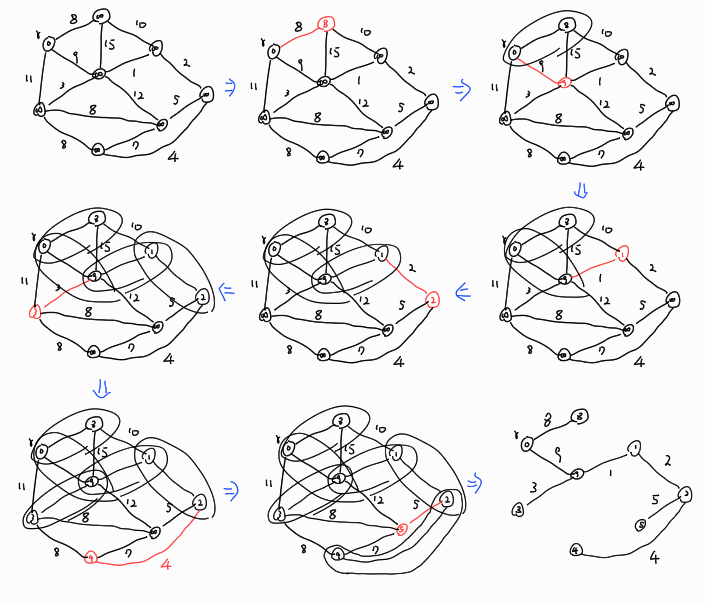
- 의사 코드는 다음과 같으며 위의 예시를 구하는 과정은 그 다음 그림과 같다.
prim(G) {
Q ← V // 우선순위 큐 Q에 모든 정점 V를 삽입
key[v] ← ∞ for all v ∈ V // V의 모든 정점 v에 대해 key값을 무한대로 지정
key[s] ← 0 for 임의의 s ∈ V // 시작 정점 s에 대해 key값을 0으로 지정
while Q ≠ ∅
// Q에 남은 정점 중 key값이 가장 작은 정점 u
u ← EXTRACT_MIN(Q)
// u에 연결된 정점 v에 대해
for each v ∈ Adj[u]
// v가 트리에 속해있지 않고 u와 v 사이의 가중치가 v의 key값보다 작다면
if v ∈ Q and w(u, v) < key[v]
then key[v] ← w(u, v) // v의 key값 초기화
π[v] ← u // v와 u를 연결
}
이해를 돕기 위해 백준 문제를 첨부한다.
https://www.acmicpc.net/problem/1197
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
크루스칼 알고리즘을 이용한 풀이
import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.List;
import java.util.ArrayList;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
class Node implements Comparable<Node> {
int from, to, cost;
public Node(int from, int to, int cost) {
this.from = from;
this.to = to;
this.cost = cost;
}
@Override
public int compareTo(Node o) {
return cost - o.cost;
}
}
public class Main {
public static void getKruskalMST(List<Node> nodes, int[] parent, int n) {
PriorityQueue<Node> pqueue = new PriorityQueue<>();
for (Node node : nodes) {
pqueue.offer(node);
}
int sum = 0, numOfEdges = 0;
while (numOfEdges < n - 1) {
Node p = pqueue.poll();
if (!isUnion(parent, p.from, p.to)) {
unionSet(parent, p.from, p.to);
numOfEdges++;
sum += p.cost;
}
}
System.out.println(sum);
}
public static void makeSet(int[] parent, int x) {
parent[x] = x;
}
public static int findSet(int[] parent, int x) {
if (parent[x] == x) return x;
return parent[x] = findSet(parent, parent[x]);
}
public static void unionSet(int[] parent, int a, int b) {
a = findSet(parent, a);
b = findSet(parent, b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
public static boolean isUnion(int[] parent, int a, int b) {
a = findSet(parent, a);
b = findSet(parent, b);
return a == b;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int v = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int[] parent = new int[v + 1];
for (int i = 1; i <= v; i++) {
makeSet(parent, i);
}
List<Node> nodes = new ArrayList<>();
while (e-- > 0) {
st = new StringTokenizer(br.readLine(), " ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
nodes.add(new Node(a, b, c));
}
getKruskalMST(nodes, parent, v);
}
}크루스칼 알고리즘을 적용하기 위해 유니온 파인드를 사용했다. Node 클래스에 대해 먼저 설명해야 할 것 같은데 Node.from 정점에서 Node.to 정점으로 가는 간선의 가중치가 Node.cost라고 이해하면 될 것 같다. 즉, Node라고 표현하긴 했지만 사실상 Edge라고 이해해도 될 것 같다.
e가 T에 추가되어 사이클을 만드는지 확인하기 위해 isUnion 메서드를 사용했다. 트리 T를 따로 만들지 않았기 때문에 numOfEdges 변수를 만들고 정점의 개수 n - 1보다 작을 때까지 while문을 반복했다.
프림 알고리즘을 이용한 풀이
import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.List;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
class Vertex implements Comparable<Vertex> {
int x, key;
public Vertex(int x, int key) {
this.x = x;
this.key = key;
}
@Override
public int compareTo(Vertex o) {
return key - o.key;
}
}
class Edge {
int to, cost;
public Edge(int to, int cost) {
this.to = to;
this.cost = cost;
}
}
public class Main {
public final static int INF = 1000000 + 1;
public static void getPrimMST(List<Edge>[] edges, int v) {
Vertex[] vertexes = new Vertex[v + 1];
vertexes[1] = new Vertex(1, 0);
for (int i = 2; i <= v; i++) {
vertexes[i] = new Vertex(i, INF);
}
int[] parent = new int[v + 1];
Arrays.fill(parent, -1);
boolean[] visited = new boolean[v + 1];
Arrays.fill(visited, false);
PriorityQueue<Vertex> pqueue = new PriorityQueue<>();
for (int i = 1; i <= v; i++) {
pqueue.offer(vertexes[i]);
}
while (!pqueue.isEmpty()) {
Vertex p = pqueue.poll();
if (edges[p.x] != null) {
for (Edge e : edges[p.x]) {
if (pqueue.contains(vertexes[e.to]) && e.cost < vertexes[e.to].key) {
pqueue.remove(vertexes[e.to]);
vertexes[e.to].key = e.cost;
pqueue.offer(vertexes[e.to]);
parent[e.to] = p.x;
}
}
}
}
int sum = 0;
for (int i = 1; i <= v; i++) {
if (vertexes[i].key != INF) {
sum += vertexes[i].key;
}
}
System.out.println(sum);
}
@SuppressWarnings("unchecked")
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int v = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
List<Edge>[] edges = new ArrayList[v + 1];
for (int i = 1; i <= v; i++) {
edges[i] = new ArrayList<Edge>();
}
while (e-- > 0) {
st = new StringTokenizer(br.readLine(), " ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
edges[a].add(new Edge(b, c));
edges[b].add(new Edge(a, c));
}
getPrimMST(edges, v);
}
}프림림 알고리즘을 적용하기 위해 Vertex 클래스와 Edge 클래스를 만들었다. Vertex 클래스를 따로 만든 이유는 key 값으로 PriorityQueue에서 우선 순위를 정해야 하기 때문이며 Edge를 ArrayList의 배열로 표현할 것이기 때문에 from은 사용하지 않고 to만 사용했다. 즉, edge[from].add(new edge(to, cost));이다. 여기서 Edge 클래스의 cost의 값은 PriorityQueue 등에서 우선순위를 비교하기 위해 사용하지 않으므로 Comparable 인터페이스를 implements하지 않았다.
또한 Integer.MAX_VALUE를 사용하지 않고 INF를 따로 정의하여 사용했는데 이유는 모르겠지만 몇몇 반례에서 작동하지 않았기 때문이다. 음의 간선이 입력값으로 들어올 때 오버플로우 문제가 발생한 것이 원인인 것 같다. 입력값에서 cost의 절댓값이 1000000을 넘지 않는다는 문제 조건 때문에 1000000 + 1로 지정했다.
Integer.MAX_VALUE 관련 오류가 발생한 것을 확인한 예제
3 3
1 2 1
2 3 2
1 2 -100출력 : -100
답 : -98
'자료구조 및 알고리즘' 카테고리의 다른 글
| SSSP(Single-source shortest paths) (0) | 2023.08.06 |
|---|---|
| 위상정렬(Topological Sort) (1) | 2023.08.05 |
| 해시 테이블(Hash Table) (0) | 2023.07.24 |
| 유니온 파인드(Union-Find) (0) | 2023.07.23 |
| 힙(Heap)과 우선순위 큐(Priority Queue) (0) | 2023.07.23 |
